2-D Math Notation vs Maple Notation

In writing Understanding Maple, I made a conscious decision to avoid a lengthy discussion of the merits and demerits of 2-D Math Input. Instead, I advised readers to switch to Maple Notation, and to perhaps give some consideration to other modes of input after learning how Maple works. I stand by this advice, but the approach has been criticised by more people than I expected (two, as opposed to none). Here, I will try to give an objective comparison of 2-D Math Input and Maple Notation. I emphasise objective, because I’ll do my best to stick to facts; it is very easy to be drawn into a fruitless, opinion-driven debate in these matters, rather like a Mac user trying to convert a Windows user, or vice-versa.

Click here if you just want to to switch off 2-D Math Input. Then there is no need to read this discussion!

Terminology

Let’s get one thing straight from the start. In 2-D Math Input, the default typeface is black and italic, and Maple tries to format mathematics as it is entered, so that typing
x
^
2
produces x2. In Maple Notation the default typeface is upright and red (or reddish brown), and the input that is typed is reproduced verbatim on the screen, so typing
x
^
2
produces x^2. Neither of these has anything to do with Worksheet Mode or Document Mode; both methods of input are available in both modes. Confusion over this terminology causes a lot of frustration for users, especially those who expect that switching to Worksheet Mode will set the default input mode to Maple Notation, and are sorely disappointed when it does not.

Finally, it's important to be aware that Maple Notation is also sometimes called Maple Input, 1-D Math Input or Text Mode. The last of these is particularly unfortunate, because Maple also has a mode for entering plain text, which is something entirely different.

Formatting equations

The most obvious difference between 2-D Math Input and Maple Notation is that 2-D Math Input is reformatted to appear as it would be written by hand, whereas Maple Notation is not. However, this is far less important than it first appears. Fractions and powers are reformatted as they are entered from the keyboard, but to get fully typeset input, one must use the palettes, and this is a very slow method of entry. It takes far longer to construct an expression such as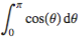

than it does to type 
int( cos( theta ) , theta = 0 .. Pi )
Furthermore, one can view a typeset version of the input by using an inert command, or by using unevaluation quotes. Thus, executing either 
Int( cos( theta ) , theta = 0 .. Pi )
or 
'int'( cos( theta ) , theta = 0 .. Pi )
entices Maple into displaying the above integral exactly as it would be written by hand, without actually evaluating it. Of course, one needs to know some syntax to perform these operations and to evaluate the integral after it has been displayed, but syntax will always be needed sooner or later, unless Maple is to be used only for solving very simple problems. There are many features that cannot be accessed using the palettes alone. The palettes also contain pitfalls for new users: why are there two different coloured subscripts in the Expression palette, and what is the difference between the integral symbols in the Calculus palette and those in the Large Operators palette, for example?

Conclusion: Debatable. The more ‘natural’ display of 2-D Math Input may be helpful in simple problems, but the full effect can only be obtained by using the palettes, which is slow, and fraught with danger for new users.

Implied multiplication

Maple Notation does not support implied multiplication. 2-D Math Input does, but one has to be very careful with spaces. For example,
2
x
will be interpreted as 2*x, but to get x*y, one must enter
x
*
y
or
x
space
y
. On its own,
x
y
will be interpreted as a single object, with the name xy. This can’t be avoided, because Maple has to assume that an unspaced sequence of letters forms a single name, or else a name such as log could end up being interpreted as l *o*g. Human mathematicians can easily see that this is ridiculous, but computers are not blessed with such intuition. Unfortunately, it is very easy to forget an asterisk (or space), and it can be difficult to see the problem from the output:
x
y
produces xy, and
x
*
y
produces x y (note the tiny space!).

Using a space to invoke implied multiplication has another drawback. If one accidentally types
c
o
s
space
(
0
)
return
the result is 0 in 2-D Math mode because Maple interprets this as the name cos multiplied by the constant 0. In Maple Notation, the space would be ignored, and the result is 1. On the other hand, a construction such as
2
(
x
−
1
)
is interpreted as an implied multiplication is 2-D Math Input, so executing this produces the result 2x−2. In Maple Notation, 2(x-1) is (somewhat counterintuitively) interpreted as the constant function whose value is 2 for all arguments, evaluated at the point x−1, so the output is simply 2.

Conclusion: Debatable, but Maple Notation is definitely simpler in this respect. Some users find implied multiplication to be a useful shortcut, but it can easily lead to mistakes. The facts that accidentally entered spaces can induce implied multiplication, and that forgotten spaces can prevent it, can be very annoying. The curious treatment of literal values preceding brackets can lead to mistakes when working with Maple Notation, but it’s easy to remember that implied multiplication never works in this mode.

Matching brackets

In 2-D Math Input, Maple will resize brackets if they contain a large structure such as a fraction. For example, typing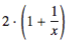
2
*
(
1
+
1
/
x
)
produces

This makes it easier to match left and right delimiters in complicated expressions, especially in cases where there are multiple sets of nested brackets (remember that only parentheses can be used to group terms in Maple expressions; square brackets and braces have special meanings, and cannot be used in this way). Brackets are not resized in Maple Notation, so the above sequence of keystrokes would simply produce 
2 * ( 1 + 1 / x )
However, in both modes, placing the cursor to the right of a closing delimiter shows the location of the corresponding opening delimiter, so it’s not usually difficult to ensure that brackets match up correctly.

Conclusion: Slight advantage to 2-D Math Input.

Extra keystrokes vs extra brackets

To move out of a fraction, exponent or subscript in 2-D Math Input, it is usually necessary to press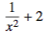
→
. Thus, to enter

one needs the sequence of keystrokes
1
/
x
^
2
→
→
+
2
. The arrows are not needed in Maple Notation. On the other hand one sometimes needs extra pairs of brackets in Maple Notation; for example x2y needs to be entered as x^( 2 * y ), but in 2-D Math Mode one can use
x
^
2
y
→


Conclusion: Tie. The need to press
→
can be annoying in 2-D Math Mode, but it eliminates the need for some pairs of brackets.

Transparency

When statements are entered in Maple Notation, Maple displays exactly what has been typed. On the other hand, the process of formatting input can make it difficult to see how a complicated expression has been entered in 2-D Math Mode. This lack of transparency becomes worse if the palettes are used. Furthermore, the fact that spaces can influence results means that Maple’s interpretation of a statement in 2-D Math Input may not be apparent from the display. Fixing problems in a malfunctioning worksheet can be extremely difficult in these circumstances. Often, the only way to repair faulty 2-D Math Input is to convert it to Maple Notation (highlight and choose
Format
►
Convert to
►
1D Math Input
 ).

Conclusion: Major advantage to Maple Notation. For anything more complicated than a single integration, displaying exactly what has been entered is an absolute must.

Function definitions

In Maple Notation, functions are defined using ‘arrow notation’; for example 

f := x -> x^2
One can read this as ‘Define f  to be the function that takes one argument, and returns the square of that argument as its result’. Note that x is a dummy variable here; exactly the same function could be defined using 
f := banana -> banana^2
A very common mistake is to enter something along the lines of 
g( x ) := x^2
This is actually a remember table assignment, which is rather different to a function definition. It says that the value of the function g for the (literal) argument x is x2. However, x is not a dummy variable in this context. If the argument is anything other than x then the function g cannot be evaluated, unless other information about it has been entered elsewhere. We can see this from the following tests: 
g( x ) := x^2
g(x) := x2 
g( x )
x2 
g( y )
g(y) 
g( 2 )
g(2) 
g( 2 * x )
g(2 x)

In 2-D Math Mode, the statements
g( x ) := x2
and
g := x → x2
are equivalent, and both define a function (at least by default; the interpretation of the former can be changed). Upon encountering a statement such as g( x ) := x2, versions up to Maple 2015 produced a dialog, warning that the input was ambiguous, and asking the user to choose a remember table assignment or a function definition. However, this was dropped in Maple 2016.

Allowing the syntax g( x ) := x2 to represent a function definition cuts out one of the most common errors made by new users. Making remember table assignments becomes more difficult, but these aren't very useful anyway. The same result can usually be achieved in a much cleaner way using a procedure. The fact that older versions of Maple issued a prompt concerning ambiguous notation means remember table assignments could not easily be programmed to operate automatically using 2-D Math Input, so the change is unlikely to break existing worksheets. However, changing the way in which syntax is interpreted from one version to another is hardly desirable. What else might change, or stop working in the future?

Conclusion: Probably a slight plus to 2-D Math Notation. A very common mistake is eliminated, at the cost of a questionable feature.

Overall conclusion

2-D Math Input can be helpful for very simple problems, especially for new users who don’t know any Maple syntax. In complicated problems (especially those that involve programming), the advantages of 2-D Math Input are largely irrelevant, but its disadvantages (lack of transparency, and the importance of spaces) can cause major problems.

Back to main Understanding Maple page