| |
Cracker |








 |
Geological outcrop studies of purely
dilational
(Mode I) fractures (e.g. joints and veins) suggest that
fractures with straight, regular fracture paths and an absence of forking to
be diagnostic of the slow, stable fracture growth associated with subcritical or quasi-static crack-tip propagation. This mode of fracturing
may be the norm under conditions of long-term loading, which are likely to
be widespread throughout the crust. Furthermore, fractures resulting from
subcritical growth have been recognised as the principal element of fracture
porosity in several hydrocarbon reservoirs. As these fractures are generally
steep, intersections by boreholes and wells are infrequent, making these
systems difficult to characterise. Thus accurate simulation of these
fracture systems can help provide geometrical templates for the
incorporation into fracture flow models and therefore may be of economic
benefit. |
|
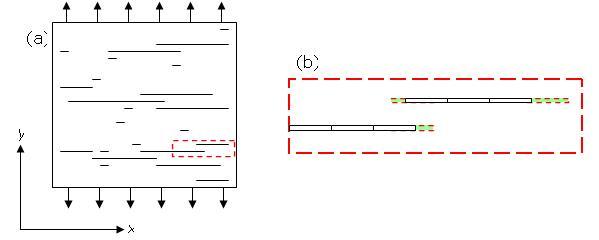
Schematic
depicting simplified modeling scheme implemented in Cracker. (a)
Simulated fracture growth is driven by uniaxial tension of a 2-dimensional
body. (b) Individual fractures represented by groups of model elements
|
|
The
Cracker software numerically simulates the growth and interaction of
Mode I fractures in 2-dimensions by implementing Linear Elastic Fracture
Mechanics theory (LEFM). A schematic of the boundary conditions used by
Cracker to simulate fracture growth is shown in Figure 1. An initial
distribution of uniformly oriented flaws of specified half-length
distribution (delimited random or constant) and spatial distribution (random
uniform or pseudo-grid) populates a finite 2-dimensional body. During each
iteration of the simulation, a constant remote uniaxial tensile stress is
simulated perpendicular to the flaws. Each model element that comprises the
fractures, the stress and extensional displacement is calculated according
to LEFM. Calculation of the stress intensity at the tip of each fracture is
determined and the crack propagated perpendicular to the applied stress by a
straight-line distance proportional to stress intensity and the specified
fracture toughness. The simulation is terminated when a specified
dimensionless fracture density or maximum fracture length is reached. |
|

|
|
Comparison of
natural subcritical fracture pattern mapped from aerial photographs with
numerical simulations of fracture patterns using Cracker. All
simulations are seeded with 50 flaws but have different fracture toughness
values (n), which result in starkly contrasting fracture patterns |
|
Fracture toughness, n, also known as the subcritical
fracture growth index, is a key variable in the numerical simulations, which
determines the sensitivity of crack-tip velocity to stress intensity at the
crack-tip. Using Cracker, it has been possible to demonstrate that
realistic fracture patterns can be simulated using low values for fracture
toughness (n ≤ 2)(Figure 2). These values are in stark contrast to
laboratory determinations of fracture toughness, which range 26-130 for
limestone rocks. The discrepancy between these determinations of n
can be rationalised by consideration of fracturing in fluid-saturated
conditions which, it is derived, must limit fracture toughness to values of
2 or less. |
|
Screen-shot
of Cracker simulating the growth of a very small number of cracks. Depending
on the parameters chosen in the input file, very many cycles may be required
to propagate the model to simulate observations. |

