Once generated, the wing-tip vortices interact with each other, the atmosphere, and, if low enough, have a complex interaction with the ground. Extensive research has been conducted in trying to understand these phenomena using a variety of methods including LIDAR and acoustic measurements as well as numerical methods to model the vortices.  These methods try to capture the characteristic behaviour of vortices such as the self-induced sink-rate, their decay, and how they are ‘transported’ by the prevailing winds. Typically, wake vortices descend at around 300-500 ft/min and can last for several minutes at near full strength in the right atmospheric conditions.  It should be highlighted that wake vortices are sensitive to the atmospheric conditions. For example, strong or turbulent winds or strong density stratification, caused by temperature gradients, are known to accelerate the decay and dispersion of wake vortices.

A number of empirical models have been used to describe the flow-field of a vortex, including such models as the Dispersion model , Burnham, Rankine and Lamb-Oseen models For this study the wake vortex model used is the ‘Burnham’ model, which takes the form:

Here, V_T is the tangential velocity which has different behaviour depending on the relative position to the vortex core. Inside the core, that is where the radial position r, is less than core radius, r_c, equation 1 is valid. Outside the core, equation 2 is used, and this models the attenuation of the velocities as the distance from the core is increased.

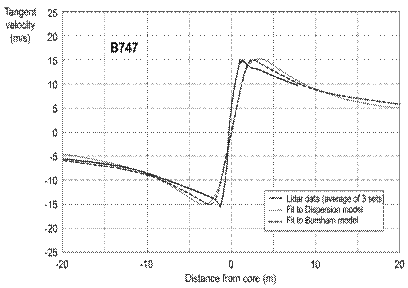
                                                                                                       Tangential velocity profile for a Boeing 747 wake vortex

The above Figure shows that a reasonably good match can be achieved using a Burnham model representation of vortex with a Boeing 747 wake measured using LIDAR (Coherent Laser Radar). The peak tangential velocity at the core radius has a magnitude of 51.45ft/s (15.68m/s), appropriate for a full strength 747 wake vortex.