
Professor Lasse Rempe-Gillen works in the field of one-dimensional holomorphic dynamics, that is, the iteration of functions of one complex variable. In particular, he is interested in the iteration of transcendental entire and meromorphic functions.
More precisely, let \(f:\mathbb{C}\to\mathbb{C}\) be a transcendental entire function; that is, a complex differentiable function from the complex plane to itself that has an essential singularity at infinity. We think of this map as describing a dynamical system, and hence study the iterates \[ f^n := \underbrace{f\circ f \circ \dots \circ f}_{\text{$n$ times}} \] of \(f\) as \(n\to\infty\).
The classical theory of holomorphic dynamics, due to Fatou, splits the complex plane into two subsets: the Fatou set, where the behaviour is stable, and the Julia set, where the behaviour is "chaotic". (The picture below shows part of the Julia set of a function of the form \(f(z)=e^z+a\), for a certain complex parameter \(a\), in dark grey, while the Fatou set is shown in colour. The black curves shown illustrate dynamically significant structures that can be found inside the Julia set.) Professor Rempe-Gillen's work, in a broad sense, is concerned with the question of understanding the structure of these sets and the behaviour of the functions on them. In particular, his work has connections with one-dimensional complex analysis (function theory) and point-set topology, particularly continuum theory.

Relevant research areas:
Recent work, in particular by Professor Rempe-Gillen, has made significant progress in understanding the topological structure of the Julia set of certain entire functions, but many questions still remain open. Recently, Mihaljevic-Brandt (while a doctoral student at Liverpool) was able to give a complete combinatorial description of the topological dynamics for a large class of "well-behaved" transcendental entire functions, each of whose Julia sets is the complex plane. (I.e., these functions are chaotic everywhere, but we can completely describe how the function behaves in combinatorial terms.) A possible PhD project would involve investigating in how far this description can be extended to larger classes of entire functions.
On the other hand, even for seemingly simple functions, such as the map \(f(z)=e^z\), the topological dynamics is still not fully understood. In particular, the following is a conjecture of Devaney from 1993. For \(a>-1\), let \(f_a:\mathbb{C}\to\mathbb{C}\) be the function \(f_a(z) := e^z+a\), and consider the set \[ \Lambda_a := \{ z\in\mathbb{C}: \operatorname{Im}(f^n(z))\in [0,\pi] \text{ for all $n\geq 0$} \}. \] This set is the closure of a countable union of curves, each of which tends to infinity in both directions, as in the following picture:
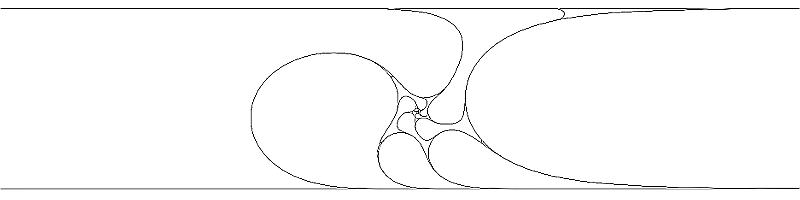
Devaney showed that this set has interesting topological properties (more precisely, it compactifies in a natural way to an indecomposable continuum). He conjectured that, for \( -1 < a < b \), the sets \(\Lambda_a\) and \(\Lambda_b\) are not homeomorphic, and this problem remains open almost 20 years later.
Resolving this conjecture is likely to be difficult, but there is an opportunity for a doctoral student to make significant progress on the problem. In particular, an interesting problem is to study the continua that arise from this construction from the point of view of continuum theory.Hausdorff dimension is an important concept that allows one to associate potentially non-integer dimensions to subsets of Euclidean space. For example, an interval has Hausdorff dimension 1, a square has Hausdorff dimension 2, while the well-known middle-thirds Cantor set has Hausdorff dimension \(\log(2)/\log(3)\), and the Sierpinski triangle has Hausdorff dimension \(\log(3)/\log(2)\).
There are many interesting results and questions regarding the Hausdorff dimension of subsets of Julia sets of transcendental entire functions, and many interesting phenomena that result from this study. In particular, let \(f\) be a hyperbolic entire function (for definitions, we refer to the relevant research articles), and let \(J_{b}(f)\) be the set of points in the Julia set of \(f\) whose orbits are bounded. A theorem proved by Professor Rempe-Gillen states that there exist such a function \(f\) for which the Hausdorff dimension of \(J_b(f)\) is equal to two, which is impossible for rational functions. On the other hand, results by Mayer and Urbanski (among others) show that for large classes of "well-behaved" hyperbolic entire functions, the Hausdorff dimension of \(J_b(f)\)is strictly less than two. A possible PhD project is to investigate this dichotomy further, and in particular to derive geometric conditions on the function \(f\) under which the Hausdorff dimension is guaranteed to be strictly less than two.
The study of Hausdorff dimension is closely connected to the measurable dynamics of the functions in question: that is, the study of natural invariant measures. (The idea is, roughly, that even though the behaviour of the map is chaotic, it may be possible to understand what the dynamics is like "on average".) There has been much work in this area recently by a variety of researchers, but many interesting questions remain open. For example, a potential thesis project could investigate the existence of natural invariant measures for examples as described above, where the dimension of the set of bounded orbits is equal to two. (Standard techniques for constructing invariant measures for hyperbolic functions fail for these examples.)