A. THE NEW ERA

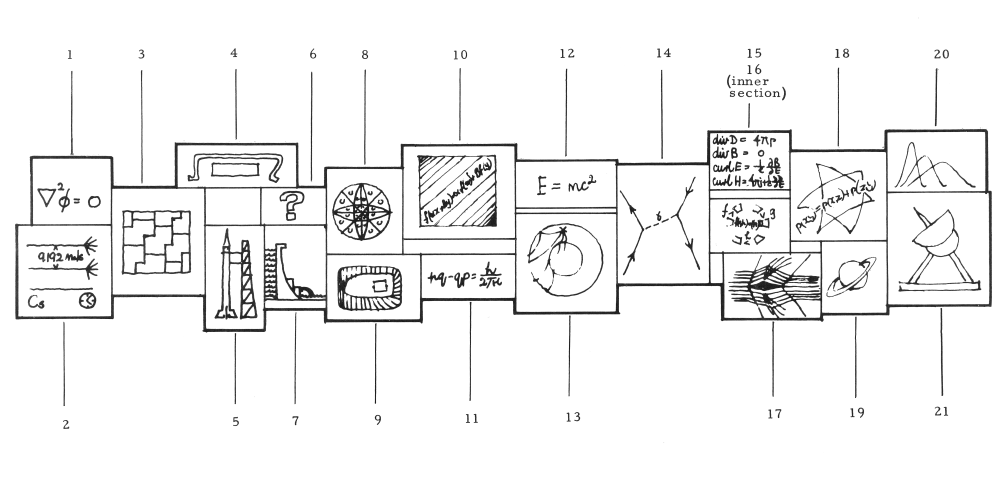
A 1. Laplace's equation:: This equation arises in many branches of mathematical physics and analytical engineering, and the study of its solutions has led to considerable advances in both pure and applied mathematics.
A 2. The atomic clock:: This clock, which depends on the constancy of a special property of the caesium atom, is a modern device for measuring time to very great accuracy.
A 3. Unsolved problems:: The problems studied by the mathematicians of the 19th century and earlier have not by any means all received solutions. The sketch here refers to the map-colouring problem, one of the celebrated unsolved problems of mathematics: - if an arbitrary map on a sphere is to be coloured in such a way that adjacent “countries” are to be of different colours, what is the minimum number of colours required? It is known that four colours are necessary for certain maps, and it has been conjectured that four are sufficient for all maps, but so far this conjecture remains unproved. Curiously, the corresponding problem for maps on the torus (or anchor-ring) has been solved, seven colours in this case being both necessary and sufficient. This sketch illustrates a map on a torus which requires seven colours (or textures), the torus here having been cut and flattened out.
Note: This problem, also known as the four-colour problem, was solved by Kenneth Appel and Wolfgang Haken in 1976. A number of other famous old problems of mathematics have been resolved in fairly recent years, such as Fermat's Last Theorem by Wiles in 1993 and the Poincaré Conjecture by Perelman in 2003. An example of a problem that remains unsolved is Goldbach's Conjecture: Every integer greater than 5 can be written as the sum of three primes.
A 4. Punched cards and paper tape for electronic computers:: This section illustrates the punched cards and punched tape which are used in modern electronic computers. These computers do arithmetic at very high speed and can be used to solve many of the mathematical problems of pure and applied science.
Note: In 1961, when the panel was unveiled, the computer revolution was just beginning. Computers in those days were large machines that received their instructions via the punched cards or tape shown on the panel. The incredible speed with which computing power has increased ever since means that today every mobile phone contains computing equipment vastly more powerful than these early machines.
A 5. Rocket at its launching station:: The giant rockets of the 20th century make possible the exploration of outer space. The design of these rockets, the calculation of their trajectories, and the interpretation of the observations obtained by scientific instruments in the rockets, all involve a very considerable use of mathematics.
Note: In 1961, the opening year of the Mathematics and Oceanography Building, Yuri Gagarin became the first person to enter space. Eight years later, Neil Armstrong was first to step on the moon.
A 6. The Future:: Many problems of pure and applied mathematics confront us now, and it is more than probable that many more such problems await us beyond the foreseeable future. The use of mathematics in science, engineering and technology is only in its infancy and there is no doubt that many new developments will arise with the growing use of mathematics in these fields.
Note: As is to be expected, the years since the opening of the building have seen vast developments in all areas of mathematics. Whole new areas of pure mathematics have emerged, and applications of mathematics are important for all sciences.
A 7. Electric power:: This illustration, which shows a dam and a pylon, refers to the ever-growing use of electric power. The design of dams, of electricity generating and distribution systems, and of electric and electronic devices, involves the use of many different branches of mathematics.
A 8. Algebraic topology:: This subject is essentially a product of the 20th century, and the considerable advances which have been made in it have had far-reaching consequences in many branches of geometry. The sketch shows an example of the triangulation of a surface, a concept which played an important part in the early development of the subject.
A 9. Differential geometry: The Möbius strip:: The Möbius strips is an example of a non-orientable (one-sided) surface. It is also a simple example of a fibre-bundle, a structure which arose in the study of differential geometry and which has played an important role in the development of many branches of modern mathematics.
A 10. Linearity:: The property of linearity represented in this sketch has, during the last 50 years, played an increasingly important part in many branches of algebra, geometry and analysis.
A 11. Heisenberg commutation equation connecting co-ordinate and momentum:: This equation is of fundamental importance in quantum theory: it is a consequence of Heisenberg's Uncertainty Principle, which imposes a limit on the degree of accuracy to which the position and momentum of a particle may be simultaneously measured. The equation reflects a radical departure from classical mechanics, according to which both the position and momentum of a particle are capable of exact simultaneous determination.
A 12. Einstein equation for the equivalence of mass and energy:: This equation was deduced by Einstein from his Special Theory of Relativity, and has been confirmed experimentally. The principle which it embodies, that mass and energy are equivalent, is of central importance in present-day concepts of mathematical physics, and has also dramatic practical consequences in the field of nuclear physics.
A 13. Earthquake waves:: Earthquake shocks travel through the earth in the form of waves and the irregular paths taken by these waves can be analysed to provide detailed information about the internal structure of the earth.
A 14. Scattering of an electron by a positron:: This sketch is typical of a class of diagrams, due to Feynman, which are used to represent processes in physics involving the scattering or transmutation of elementary particles.
A 15. Maxwell's electromagnetic equations:: These equations are of fundamental importance in the theory of electromagnetic phenomena, and have numerous scientific and industrial applications. They provide, for example, the mathematical theory for the transmission of radio waves and also that for the generation of magnetic fields by the passage of electric currents in wires.
A 16. Mappings:: A mapping from one set to another is a straight-forward generalization of the idea of a function. The theory of abstract groups arose from the study of groups of mappings of a set onto itself under a particular form of multiplication, and the sketch symbolises this multiplication of mappings.
A 17. Shock waves and the motion of fluids:: The sketch shows the formation of shock waves when a body with sharp leading and trailing edges passes through a fluid at supersonic speed. Our understanding of the motion of fluids has been considerably sharpened by a combination of mathematics and experimental observations.
A 18. The triangle inequality:: The relation which appears in this sketch is known as “the triangle inequality”: if ρ(x, y) denotes the distance from x to y, then the relation expresses the fact that the direct distance from x to y is less than or equal to the distance from x to y via any third point z. This relation, together with two other relations of a somewhat similar character, is used to define a generalized “distance” which includes Euclidean distance as a particular case. Such generalizations of Euclidean distance occur in many situations in pure mathematics, and all these instances can be dealt with by a single theory which examines properties of a “distance” defined axiomatically by the three relations mentioned. Such a use of an axiomatic definition of a general concept to include a large number of special cases is one of the most characteristic features of modern pure mathematics.
A 19. Astronomy:: The sketch refers to our greatly increased understanding of distant heavenly bodies. The development of the theories on which our understanding is based, and the cross-linking of observation with theory, depend to a very great extent on the use of mathematics. For example, our understanding of the mechanism of Saturn's rings depends largely on a synthesis of mathematical and observational arguments.
A 20. Mathematical statistics:: The sketch shows three normal distribution curves with different centre and spreads. Such curves are commonly used to describe the variations observed in experimental data. Some of the distributions of measurements which they describe may also be predicted on theoretical grounds. The growth of the use of statistical ideas in many branches of science, engineering, and business administration has been one of the remarkable features of 20th century applied mathematics.
A 21. Radio telescopes:: These constitute the most important recent addition to the equipment of astronomers. The observations which are being made with them are opening up new avenues of thought concerning the nature of the universe.

B. THE DEVELOPMENT OF MEASUREMENT

An eclipse of the moon is shown on the left, and one of the sun on the right. The angular diameters of the sun and the moon happen to be approximately equal, but the angular diameter of the earth's shadow cast on the moon is considerably greater. The ancients gave considerable attention to eclipses, but the motion of the moon is so complicated that only in modern times has prediction of eclipses become reasonably precise - through the massive use of mathematics.

B 2. Measurement and the human figure:

Early units of length are often related to the human figure, standing or marching. For example, the biblical cubit is connected with the length of the forearm.

B 3. Early Egyptian fractions:

In dealing with fractions, the early Egyptians almost always restricted themselves to those fractions which have unity in the numerator. The symbol for “one part of” was

while

and

denote one and ten respectively. The fractions shown in the sketch are:

¹⁄₆ ¹⁄₇ ¹⁄₈

¹⁄₉ ¹⁄₁₀ ¹⁄₁₁

All calculations are difficult without some simple notation, and in all the early civilisations scientists were hampered in their work because their notations were suitable only for the simplest of calculations.

B 4. Liquid and grain measures:

Early measures of capacity arose from the practical need to standardize quantities of liquid and grain for the purposes of trade and commerce.

B 5. Lion and duck weights:

Weights of these forms, made of metal, stone or marble, have been found in Mesopotamia. Metal weights were adjusted by the removal of material from the base or by the packing of material into spaces within the weights. It is thought that they were used during the period from about 5000 B.C. to about 500 B.C.

B 6. Orientation by the sun:

The accurate determination of the cardinal points is essentially an astronomical process. The north-south direction can be found from the shadow of a vertical stick at noon, when the length of the shadow is least. A more accurate method is illustrated in the sketch: this uses morning and afternoon shadows of the same length. During the day, the shadow of the top of the stick traces out on the ground a branch of a hyperbola, which intersects a circle centred at the bottom of the stick in two points whose join defines the east-west direction; the north-south direction is perpendicular to this.

B 7. Greek currency:

From early times it has been necessary to measure quantities of gold, silver and other metals, and to practise the arithmetic of currency systems and “foreign exchange”.

B 8. Measurement of pyramid:

The height of a pyramid may be found from the length of its shadow and the length of the shadow cast by a vertical stick of known length, using the properties of similar triangles.

B 9. Part of a Babylonian multiplication table:

The top line and left-hand column contain what we now call the “arguments” of the table. The portion shown reads:

1 2
1 1 2
2 2 4
3 3 6
4 4 8

B 10. Estimation of the area of a circle:

The area of the circle is less than that of the circumscribed hexagon and greater than that of the inscribed hexagon. From these two facts it can easily be deduced that π lies between 3 and 3.4641.

B 11. Scales:

Standards of weight were prescribed in very early times.

B 12. Triangulation of land:

An easy way of measuring the area of a field whose boundary consists of a number of straight portions is to divide the field into triangles. The annual flooding of the Nile compelled the early Egyptians to give much attention to land measurements.

C. THE RECORDING OF TIME

C 1. Part of Maya stele:: The Mayas of Central America, whose first Empire flourished from the 2nd to the 7th century, had a remarkable number system. They carved dates on stone columns (known as steles) using special numerals shaped like human faces. Their calculations of time were based on a sun calendar of 365 days which they invented.
C 2. Sundial:: An early device giving daily and seasonal records of the passage of time based on the motion of the sun.
C 3. Clocks:: The crude weight-driven clocks of the middle ages were in their day a great invention, but for the accurate recording of time over long periods they were of no more uses than the earlier candle-clocks, sun-dials and hour-glasses. The more accurate time-measuring clocks of later centuries were operated by springs or electricity.
C 4. Chinese astronomy:: The Chinese gave much attention to astronomy, and descriptions of celestial phenomena in Chinese records form an invaluable addition to those in western chronicles.
C 5. Halley's comet, from the Bayeux tapestry:: The comet thus fancifully depicted is approximately periodic in its returns. It is known to have made 11 revolutions round the Sun in the interval between 1066 and 1910, and its next appearance is due about 1986.
C 6. The Moon:: The average length of the “lunation” between successive new moons is about 29.5306 days, and approximations to this have figured in the calendars of various peoples.
C 7. Hour glass:: This was a once common means of indicating the passage of time.
C 8. The Seasons:: These occur because the plane of the Earth's equator is inclined at about 23.5 degrees to the plane of the “ecliptic” in which the Earth moves round the Sun.
C 9. The Sun:: A fanciful representation of the Sun, whose annual apparent circuit of the heavens determines the length of the year.
C 10. Daily motion of the stars:: In consequence of the Earth's rotation about its axis, the stars appear to rotate once a day about the north pole of the heavens - this diurnal motion of the stars has been important in the measurement of time from very early days. The sketch shows the Pole Star, which at the present time marks approximately the position of the north pole of the heavens, together with the principal stars of the constellation of the Great Bear.
C 11. The number of days in a year:: There are about 365.2422 mean solar days in a “tropical year”, which keeps in step with the seasons. In the Gregorian calendar of 1582, which has been used in this country since 1752, years divisible by 4 are leap years, except that a centennial year is a leap year only if it is divisible by 400. Thus there are 97 leap days in 400 years, which give an average of 365.2425 days in a calendar year; this calendar is sufficiently precise to enable it to be used with confidence for several thousand years yet.

D. THE INFLUENCE OF GREECE AND ROME

D 1. Platonic inscription:: It has been said that Plato wrote over the entrance to his Academy “Let no one ignorant of geometry enter my door”.
D 2. Ruler and compasses:: In the solution of problems which required a geometrical construction, the early Greek geometers allowed themselves the use of various mechanical devices for constructing curves. The use of any instruments other than a ruler and a pair of compasses was objected to by Plato, on the grounds that it destroyed the value of geometry as an intellectual exercise, and his opinion carried such weight that it was at once adopted as a canon to be observed in such problems.
D 3. Pappus' Theorem:: The theorem illustrated by this sketch, which is due to Pappus, states that if A, B, C are any three distinct point on one line, and A', B', C' are any three distinct points on another, then the points of intersection of the lines AB', and A'B, BC' and B'C, and CA' and C'A, are collinear. The theorem, which is one of the earliest geometrical results of a non-metrical character, was proved by Pappus within the framework of Euclidean geometry, but the result belongs properly to projective geometry and there its true significance was only realised in the later half of the 19th century.
D 4. The Theorem of Pythagoras:: The rule for laying out a right angle by making a triangle with cords of certain specified lengths was well-known to the master-builders of ancient Egypt, even before the time of Pythagoras. The achievement of Pythagoras lay in the proof of the general theorem, irrespective of the lengths of the sides of the triangle - a masterpiece in the science of deductive geometry.
D 5. Greece:: The sketch of a Greek temple symbolises the influence of Greece. We have inherited from the Greeks our ideas of systematic logic and proof, and the idea that the physical phenomena of our world are connected by some underlying pattern of logic.
D 6. The rectangle property of a circle:: The sketch illustrates the theorem that if AB, CD are two chords of a circle which intersect at a point E, then the product of the lengths AE, EB, is equal to the product of the lengths CE, ED. This theorem is one of the many results concerning the circle discovered by the Greek geometers.
D 7. Rome:: This representation of a part of the Colloseum symbolises the influence of Rome. The Romans contributed very little to abstract mathematics, but made considerable use of mathematics in architectural and engineering problems.
D 8. Greek ideas on the solar system:: The Greek astronomers regarded the earth as the centre of the solar system and they considered the motion of the sun and the planets only relative to the earth. The sketch illustrates the motion of the planet Jupiter relative to the earth - the path is an epicycle which does not close (Jupiter goes round the sun in about 11.86 years, so that the epicycle has about 10.86 loops in a complete revolution, a fact which was known to the ancients). The assumption that the earth was the centre of the solar system proved an effective barrier to the creation of a general theory explaining the motion of the planets, and it was not until the conjecture of Copernicus was accepted - that the sun is the centre of the solar system - that a general theory was developed.
D 9. Ionic and Roman numerals:: The first and third lines contain Greek letter-numerals, the second and fourth contain Roman letter-numerals. In the Hindu-Arabic notation which is now most commonly used, the numbers depicted in each of the top two lines are 1, 2, 3, 4, 5 and those in each of the bottom two lines, 10, 50, 100, 500, 1000.
D 10. A conic section:: The conic sections, i.e. the curves which are obtained by plane sections of a doubly-infinite cone, were first studies by Menaechmus. The sketch shows a hyperbola, the curve which is obtained when the plane section meets both parts of the cone without passing through the cone's vertex. Most of the metrical properties of the conic sections were discovered by Apollonius, whose treatise on this subject has been described as the crown of Greek geometry.
D 11. The Archimedean Spiral:: In the Archimedean spiral, the vectorial angle and radius vector both increase uniformly. As its name implies, this curve was first studied by Archimedes. In particular, Archimedes determined the area of the region enclosed between the curve and two radii vectores (in the sketch this region is recessed); in this work he anticipated some of the ideas of the integral calculus developed nearly 2000 years later by Newton and Leibniz.
D 12. The Pythagorean philosophy:: The Pythagorean Brotherhood laid it down as an article of faith that integers had mystical significance. Integers assumed additional significance of this kind when Pythagoras found experimentally that the lengths of strings which gave a note, its fifth and its octave, were in the simple ratios 6: 4: 3. From this fact the Pythagoreans developed mystical ideas associated with music also.
D 13. Plane section of a torus:: The curves which are obtained by plane sections of a torus, or anchor ring, belong to the class of lemniscates. They were first studied by Eudoxus, who used them, in a manner not now known, in an attempt to explain the motion of the planets.
D 14. Equiangular triangles:: The theorem that corresponding sides of two equiangular triangles are proportional to each other seems to have been discovered by Thales, the earliest of the great Greek geometers. According to Plutarch, it was Thales who, on a visit to Egypt, showed how this theorem could be used to obtain the height of a pyramid (cf. B 8.).
D 15. Achilles and the tortoise:: The famous paradox concerning a race between Achilles and a tortoise was enunciated by Zeno, one of the most prominent members of the Eleatic school of c. 460 B.C. Zeno argued that if the tortoise had a start, then Achilles could never overtake it. For example, if Achilles ran ten times as fast as the tortoise, and the tortoise had 1000 yards start, then when Achilles had run the 1000 yards, the tortoise would still be 100 yards in front of him; by the time he had covered these 100 yards it would still be 10 yards in front of him; and so on for ever.
D 16. Archimedean screw:: Archimedes, the greatest mathematician of his age, also invented many mechanical devices including the screw now known by his name. The Archimedes screw was used in Egypt to drain fields after an inundation of the Nile; it was also frequently used to pump water out of ships.
D 17. Archimedean tomb symbol:: The Romans erected a splendid tomb to Archimedes on which was engraved (in accordance with a wish he had expressed) the figure of a sphere inscribed in a cylinder, in memory of the proof he had given that the volume of a sphere was equal to two-thirds that of the circumscribing cylinder, and its surface to four times the area of a great circle.
D 18. Ellipse and its evolute:: The evolute of the ellipse (i.e. the curve traced out by the centre of a curvature of the ellipse), together with the evolutes of the hyperbola and parabola, were discussed by Apollonius in his treatise on the conic sections.
D 19. The principle of Archimedes:: Archimedes is supposed to have discovered this famous principle of buoyancy while trying to find whether a crown submitted by a royal goldsmith was made entirely of gold or a mixture of gold and silver. The achievements of Archimedes in this field of hydrostatics were such that no significant advance was made on his treatment of the subject until the work of Stevinus some 1850 years later.
D 20. Focus-directrix property of a conic:: The focus and directrix of a conic are respectively a point and a line; they have the property that the distance of any point of the conic from the focus bears a constant ratio to the distance of this point of the conic from the directrix. The focus-directrix property was discovered by Pappus, the last of the great Greek geometers, about the year 340 A.D.

E. FROM ROME TO THE 19TH CENTURY

E 1. Positional numeration:: The development of positional numeration by the Hindu mathematicians about the 7th century A.D. led to very considerable simplifications in the ordinary processes of arithmetic. In the system of positional numeration any number is represented by a sequence of symbols; the value assigned to any symbol in the sequence depends on both its “face value” and its position in the sequence (e.g. the first 3 in the number 3034 shown here stands for 3000, the second 3 for 30). This system was almost certainly derived from the abacus or counting-board, and a crucial step in this derivation was the recognition that a symbol was required for the empty column.
E 2. Differential and integral calculus:: The introduction of the differential and integral calculus by Newton and Leibniz may be said to have begun the modern era in mathematics. On the one hand it led to the creation of the subject of analysis, which formed the major occupation of pure mathematicians in the 18th and 19th centuries, while on the other hand it made possible the theoretical treatment of the most complex physical situations, and so turned the subject of mathematical physics from a collection of isolated results to a significant discipline involving mathematics and physics.
E 3. Influence of the East:: Arab and Hebrew travellers and learned men brought into Europe the mathematics and the science of the East, and by their discussions with philosophers in the West greatly influenced the further development of mathematics and science. Our formal and systematic knowledge of Eastern science and mathematics was introduced into Europe principally through the Moorish Universities of Granada, Cordova, and Seville.
E 4. Projective geometry:: The origins of projective geometry are to be found in the writing of the Greeks. Significant notions which led to its development include the introduction of points at infinity, due to Desargues, and the systematic use of imaginary points, due to Poncelet. It was not until the middle of the 19th century that mathematicians insisted that projective geometry should be built on a foundation in which metrical ideas had no part. The diagram illustrates a famous theorem of projective geometry due to Poncelet, which states that if two conics S and S' are such that there exists a triangle whose vertices lie on S and whose sides touch S', then there is an infinity of such triangles.
E 5. Tartaglia's solution of the cubic:: The modern symbolic treatment of algebra began with the Italian school at the time of the Renaissance. One of the early members of this school was Tartaglia, who is best known today for his solution of the cubic equation. Tartaglia reduced this problem to that of finding two cubes, given the product of their sides and the difference in their volumes, a problem which in turn can be reduced to the solution of a quadratic equation.
E 6. Pendulm:: In 1583, a young Italian medical student, Galileo, watched a lamp swinging backwards and forwards in the Pisa Cathedral. Timing its motion by the beat of his own pulse he found that, within the accuracy of his measurements, all swings took the same time whether they were large or small. From this simple observation, which was subsequently confirmed much more accurately, there grew much mathematics as well as the theory of vibrations and a great body of knowledge and ideas which are fundamental to much of modern physics and engineering.
E 7. New symbols:: The sketch shows some of the symbols introduced during the period covered by this panel. It includes the symbols for the ordinary arithmetical operations, the symbols of equality and inequality, the operational symbols of the differential and integral calculus, the functional symbols for the elementary functions of analysis, and the symbol for a matrix.
E 8. Galileo:: Galileo showed by direct experiment that if he dropped two different weights simultaneously from the high gallery of the Leaning Tower of Pisa, both the heavy weight and the light one hit the ground at the same time. This was contrary to the accepted views of contemporary scientists - but the experiment was conclusive and started that revolution in dynamics and astronomy which is principally associated with the names of Newton and Einstein. In the growth of this revolution mathematics and observation marched forward side by side.
E 9. Transverse vibrations of a string:: The simple mathematical investigation of the way in which a string vibrates transversely led to the formulation of the basic differential equation of wave motion - one which lies at the heart of many branches of physics and engineering, and which has given rise to much mathematics.
E 10. Navigation:: The need to be able to navigate the oceans with confidence was one of the prime requirements of all adventurous developing nations. The experience gained in voyages over the sea led to an acceptance of the idea that the earth was curved and not flat as laid down by ancient authority. There also arose the requirement of determining accurate “local time” at sea, but the solution had to wait to the early part of the 18th century when Newton and Hadley invented the sextant for this purpose. In all this development social needs, accurate observation, and mathematical developments were combined.
E 11. 15th century arithmetic:: By the 15th century the growth of commerce required text-books of commercial arithmetic. The Hindu system of numeration was brought into Europe by Arabian mathematicians and the panel depicts a calculation carried out in the “new notation”. It shows 237 x 146 = 34,602.
E 12. Hooke and the Law of Extension: CEIIINOSSSTTUV:: In 1676 Hooke propounded this anagram. Many years before he had set himself the problem of finding the relationship between force applied to a solid body and the resulting deformation. Years of work brought him to the conclusion contained in the anagram. It was only two years afterwards that he supplied the solution “Ut tensio sic vis” - “The extension is proportional to the force”. This relation led to the development of ideas which are fundamental in many branches of engineering.
E 13. The development of mathematical analysis:: The formula which appears in the sketch is that for a Taylor series, and was first discovered by Taylor about the year 1716. The treatment of this formula during the period under consideration typifies the development of the subject of analysis itself. There was first Taylor's own unrigorous treatment in the early days of the calculus, then a more rigorous treatment by Lagrange and others during the late 18th century. In 1831 the formula was extended by Cauchy to functions of complex variable, and finally in the second half of the 19th century it became the foundation of Weierstrass's theory of general analytic functions.
E 14. Gravitational attraction:: Newton's famous idea that the sun pulls planets towards itself in exactly the same way that the earth pulls apples towards itself, opened up the way for the development of the mathematical theory of modern dynamical astronomy.
E 15. Cartesian geometry:: The introduction of a co-ordinate system in geometry is due to Descartes in 1637. He is said to have made his discovery in the course of a solution to a problem proposed by Pappus: - To find the locus of a point which moves so that the product of its distances from two fixed straight lines bears a fixed ratio to the product of the distances from two other fixed straight lines. The locus is a pair of conics, and the sketch shows a typical case.