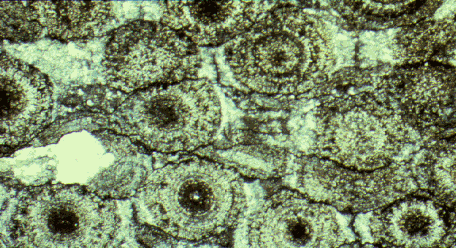
Modelling grain boundary diffusion creep in monomineralic and polymineralic rocks

This project was undertaken by Dr. Judy Ford and John Wheeler in 2001-2002 and the modelling has been developed since by John Wheeler. Pressure solution, or in dry rocks, Coble creep, is the deformation of material in response to applied stresses by diffusion along grain boundaries. It is an important mechanism in rock deformation, but is not yet well understood. It is also of great interest to materials scientists who are concerned with the strength of materials under stress. In particular, our research is relevant to the deformation of power rods in nuclear reactors and to superplastic flow of metals and ceramics.

Here originally spherical objects have been shortened by dissolution at the top and bottom surfaces. That dissolved material (calcite, CaCO3) has moved and precipitated at the side surfaces.

Simulating single-phase grain boundary diffusion creep: finite microstructure with edges

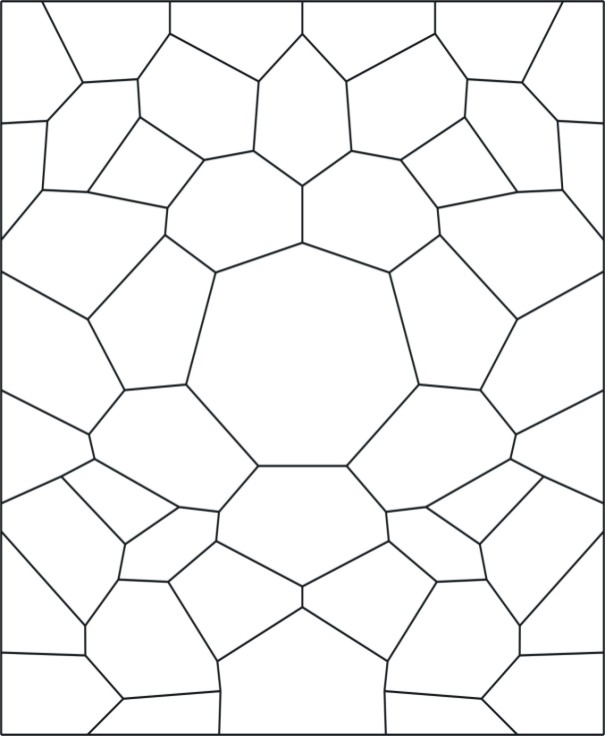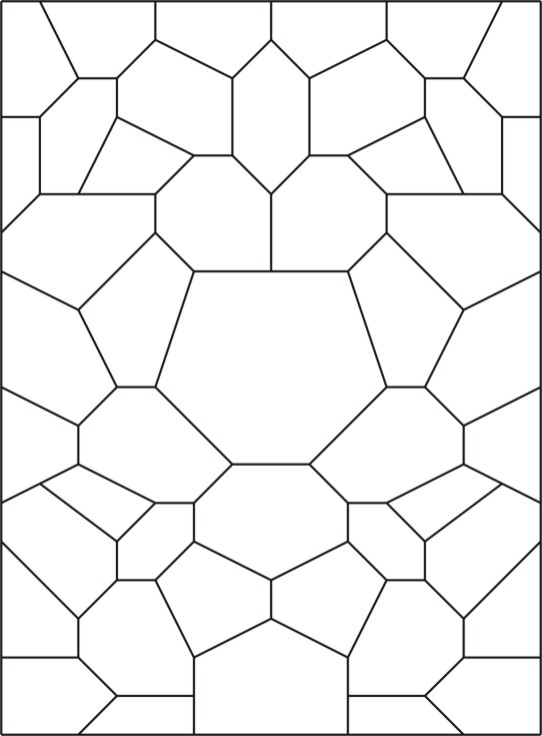
			The stress distribution and grain movements in a single-phase polycrystal can be modelled in terms of cubic functions along each grain boundary and this enables us to simulate deformation of single-phase materials under applied stress. This sequence of pictures from our simulation program shows grain-shape changes in a polycrystal made up of irregular grains. Here we have imposed a constant downward velocity on the grains at the top surface and constrained the sides of the polycrystal to maintain a rectangular shape. Animation of evolution of grain boundary network. Velocity of top and side grains fixed.
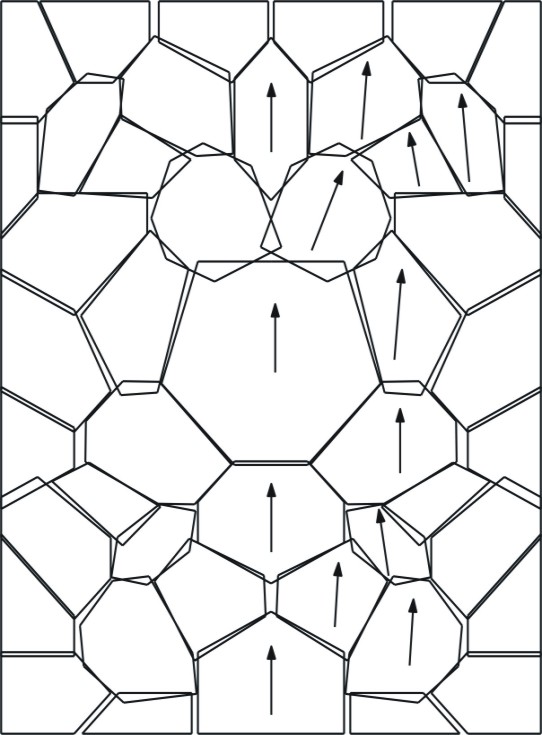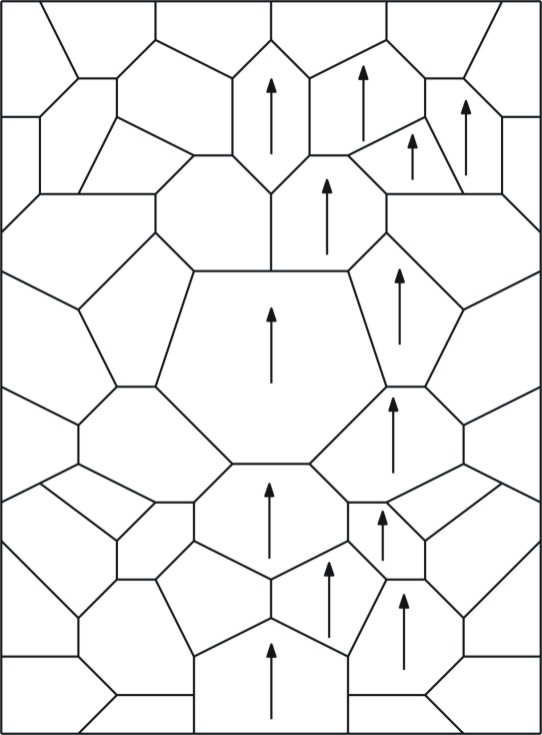
		We can also monitor the movement of individual grains, by tracking the original grain outlines. On left you can see how some grains undergo considerable rotation under externally applied stress. Notice particularly the two grains immediately above the large central grain. Because of the longer diffusion distances, large grains deform more slowly than small ones. The result is that the grains rotate so that they can slide around the larger grain. Animation of outlines of original grains. This shows more clearly where precipitation or dissolution have occurred. Note also the rotations of grains just above the central grain.	Here are some of the model assumptions: Normal stress should be continuous everywhere including triple junctions. Fluxes at triple junctions should sum to zero. Since flux is proportional to stress gradient, this means that there should always be gradients in and out of any triple junction. The program DiffForm was written in C by Judy Ford in 2001-2 and modified since by John Wheeler The Matlab viewing routines in DiffView were written by John Wheeler, 2003 onwards
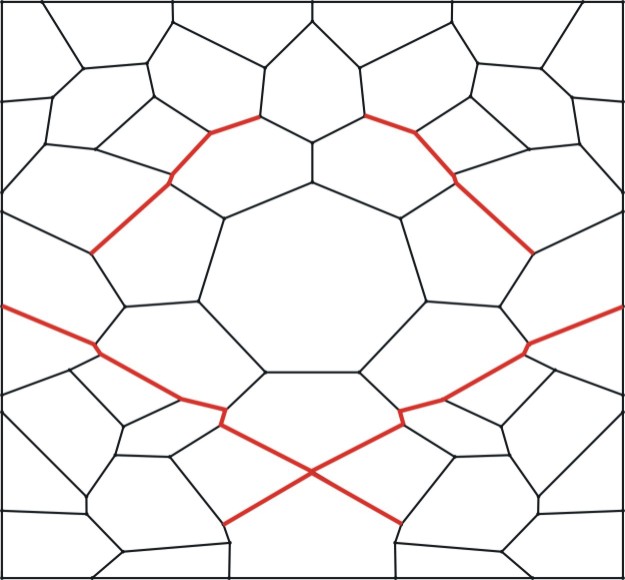	Eventually some grain boundaries become so short that nodes collide, as in the picture left. This leads to a "neighbour switching" event, in which the left and right grains part company and the top and bottom grains come into contact. This involves a change in the topology of the network, and was somewhat of a challenge to implement. Notice how some grain boundaries are starting to become aligned, making it easier for grains to slide past one another. It is also noteworthy that the large central grain has not become elongated perpendicular to the applied compressive stress. The ease of diffusion creep is grain size dependent, so this large grain is in a sense more rigid than its surroundings.	VRML file of the normal stress system (for frame 3 of this model). This allows one to spin, zoom and pan the 3D model and view the stress system in detail. To view this you need a VRML viewer or plugin, for example Cortona.	Animation of stress system. This is shown as a view of a three-dimensional picture with the stress values plotted along the z-axis. Only the normal stress at the grain boundaries are relevant, and these are usually nearly parabolic. The colour coding indicates the rate of dissolution or precipitation. Dissolution is in blue, precipitation in green. A boundary between grains which are not rotating will have a single colour. A boundary between rotating grains will show colour variation.

Simulating single-phase grain boundary diffusion creep: periodic microstructure with no edges

By the mid 2000s it was clear that the finite microstructures such as that above were limited in what they could show because their behaviour is strongly influenced by boundary conditions. So I implemented periodic microstructures and boundary conditions. This was tricky. Here is an animation colour coded by angular velocity and showing many neighbour switching events.

Want to know more?

Ford, J. M., Wheeler, J. & Movchan, A. B. 2002. Computer simulation of grain boundary creep. Acta Materialia 50, 3941-3955.

Ford, J. M., Ford, N. J. & Wheeler, J. 2004 in press. Simulation of grain boundary diffusion creep: analysis of some new numerical techniques. Proceedings of the Royal Society of London Series A.

Berton, J. R., Durney, D. W., Wheeler, J. & Ford, J. M. 2006. Diffusion-creep modelling of fibrous pressure-shadows. Tectonophysics 425, 191-205.

Wheeler, J. 2009. The preservation of seismic anisotropy in the Earth’s mantle during diffusion creep. Geophysical Journal International 178, 1723-1732.

Wheeler, J. 2010. Anisotropic rheology during grain boundary diffusion creep and its relation to grain rotation, grain boundary sliding and superplasticity. Philosophical Magazine 90, 2841-2864.

Wheeler, J. & Ford, J. M. 2007. Diffusion Creep. In: Microdynamic simulation – From microprocess to patterns in rocks (edited by Bons, P. D., Jessell, M. & Koehn, D.). Lecture Notes in Earth Science. Springer, Berlin / Heidelberg, 161-169.

A first attempt at simulating 2-phase grain boundary diffusion creep

Ford, J. M. & Wheeler, J. 2004. Modelling interface diffusion creep in two-phase materials. Acta Materialia 52(8), 2365-2376.

Last Updated: 2 April 2004